Saskia de Winter

swinter@aw.sgi.com

Desde hace mas de cien años, los matemáticos que se habían to pado con los fractales los consideraban monstruos de una irregularidad insospech able. Pero no es hasta 1977-1982 que el profesor Benoit Mandelbrot explicó que p recisamente esta irregularidad insospechable es lo que conforma a la naturaleza, y que por lo tanto es nuestra esencia misma: los que nos constituye. La geometr ía fractal se dedica al estudio de las figuras con infinito detalle que describe n algunos fenómenos naturales. Es la ciencia inherente de lo impredecible. Los f ractales cumplen en general con tres caraterísticas importantes:

1. Se basan en una geometría compleja y de infinito detalle; es decir, podemos aumentar mil es de veces el lente de nuestra cámara, y seguiremos viendo tanto detalle aproxi madamente como el que tenía la figura original.
2. La información que los g enera es relativamente poca, y en particular se basan en un principio de retroal imentación de los resultados creando iteraciones que dependen de los parámetros de entrada. Normalmente se manejan números complejos. (Un número complejo es aqu el que se compone de una parte real y de una parte imaginaria).
3. La mayor ía de los fractales cumplen con el principio de "similitud a si mismos" (self-si milar). Un ejemplo de la naturaleza es un brócoli. Al mirar el brócoli, se obser va que es una verdura con un tronco y con un grupo de "florecillas" en la parte superior. Pero curiosamente, al mirar con mas cuidado, se observan tallos mas de lgados con sus respectivas "florecillas" que a su vez se constituyen por tallos aún mas delgado y florecillas mas pequeñas. Precisamente la característica de re alizar "zooms" en los fractales se le conoce con el nombre de similitud a si mis mos. De la misma manera podemos observar un helecho compuesto de un tallo con su s respectivas hojas, una nube conformada de nubes mas pequeñas, o bien una monta ña constituída por montañitas.

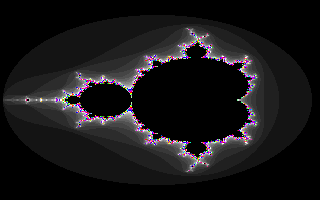
Existen varios fractales que son ya famosos por sus características. El mas famoso de todos ellos es el conjunto de Mandelbrot. La formula que describe al conjunto de Mandelbrot es:

znuevo=zv iejo*zviejo + c

donde z es un número complejo (Ej. 9+3i) y c es una constante (Ej. -0.122 + 0.745i). En realidad, el conjunto de Mandelbrot se le c onsidera una especie de diccionario que describe a otros fractales llamados los conjuntos de Julia. Siempre se comienza con z=0. La pregunta a contestar es si d espues de un cierto número de iteraciones dada la constante c, el resultado tend erá a infinito o no. Si el resultado es infinito, entonces en el plano complejo se colorea esta constante de algún color. En cambio, si el resultado tiende a un valor, se colorea de otro. También, según el número de iteraciones antes de lle gar a un resultado no infinito se puede escojer un color. Al final, el plano com plejo queda como la siguiente figura:

Otro fractal muy famoso es el triángulo de Sierpinsky. E ste fractal se construye al utilizar un triángulo como parámetro inicial, y posteriormente iterando las siguientes reglas:1) Se escala el objeto a la mitad2) Se repite el objeto tres veces: una en la parte inferior izquierda, otra en la parte inferior derecha y la última en la parte central superior.Despues de una primera iteración se obtiene como resultado una figura construida por tres triángulos. Despues de la segunda iteración serán nueve. Despues de la tercera serán 27, etc.

Esta figura además tiene varias características dignas de estudio. No importa con qué figura se comienza ( un triángulo,un cuadrado, una cara, un barco, etc) Si se siguen las reglas, despues de un cierto número de iteraciones siempre se obtendrá la misma figura: El triángulo de Sierpinsky. Es un objeto con dimensión fractal de 1.58. Esto quiere decir que es un objeto que tiene dimensión mayor a una línea recta (dimension=1) y una dimensión menor a la de un cuadrado (dimensión=2). ¡Entonces en la naturaleza existen objetos con dimensión fraccionaria! ¡Estan entre una línea y el plano o bien entre el plano de dos ejes y el plano de tres ejes (entre un cuadrado y un cubo)! Y por lo tanto, existen fractales con dimensión 4.23, 5.02, etc.

Existe aún mucho material por ahondar en la geometría fractal, que además está íntimamente relacionada con la teoría del caos. El caos es un comportamiento que aparentemente es impredecible y que se surge dentro de un sistema determinístico por ser muy sensible a las condiciones iniciales. Lo importante es que ya comenzaron a aplicarse los conocimientos teóricos, como por ejemplo para la comprensión fractal de imágenes. Y en especial para la comunidad de la computación gráfica, ahora ya se puede pensar que los fractales no solamente hacen texturas espectaculares de mármoles o de nubes. También hacen triángulos extraños, y copos de nieve con detalle infinito.